Off and on, I get this urge to work with hyperparameter optimization. I first realized that there were better approaches for doing this than plain grid search about a year ago, when I read about Bayesian Hyperparameter search. Around that time I described an experiment using Bayesian Hyperparameter search to choose optimal parameters for a scikit-learn Random Forest classifier. Few months later, I wrote about another experiment where I used it against a Spark Logistic Regression based classifier.
In both these approaches, I used an acceptance function to compare each solution against the previous solution. While this does lead to optimal or near-optimal solutions most of the time, one of the advantages of grid search is that they can all be run independently, so if you have sufficient compute capacity you can run them in parallel. Using an acceptance function forces the searches to be sequential, since the current search depends on the previous search.
Around the same time, a colleague sent me a link to the paper Random Search for Hyper-Parameter Optimization by Bergstra and Bengio, where the authors show empirically and theoretically that random search is more efficient for parameter optimization than grid search. Having seen first hand the gains one can get with random search with acceptance functions, I was on board with it out-performing grid search as long as we used some form of acceptance function, but I couldn't quite wrap my mind around pure random search doing the same thing.
In any case, since that time, I have used a combination of sparse grid search followed by a more focused manual search when I needed to find the best parameters for my model, so I didn't think too much about random search. Quite recently, however, when driving through some particularly scenic countryside (winter landscapes in the East Bay of Northern California, where I live, are extremely beautiful, especially when it has just stopped raining), I had an idea as to how I might test this for myself, and perhaps convince myself (or otherwise) about the effectiveness of random search. This post describes the idea, the implementation and the results I got from it.
The experimental setup I came up with was as follows. My hyperparameter space would be a two dimensional space of size (1024, 1024), and represented by a matrix of the same shape. Our budget for finding the best hyperparameter setting is 25 experiments. So this would allow us to do a grid search where we consider combinations of 5 values of each hyperparameter, or alternatively 25 random searches in that space. In addition, I consider a "batched" version of random search, where I execute 5 batches of 5 random searches, refining the search after each batch. I generate many such random hyperparameter spaces and count how many times the two varieties of random search outperform grid search.
Generating the space
The idea is to generate random 2D hyperparameter spaces, ie, some kind of terrain. I used the Terrain Generation Tutorial: Hill Algorithm from robot frog: 3d. Its a simple and elegant algorithm, and very well explained. My Python implementation looks like this:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | from __future__ import division, print_function
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import operator
%matplotlib inline
SIZE = 1024
NUM_ITERATIONS = 200
terrain = np.zeros((SIZE, SIZE), dtype="float")
mod_iter = NUM_ITERATIONS // 10
for iter in range(NUM_ITERATIONS):
if iter % mod_iter == 0:
print("iteration: {:d}".format(iter))
r = int(np.random.uniform(0, 0.2 * SIZE))
xc, yc = np.random.randint(0, SIZE - 1, 2)
z = 0
xmin, xmax = int(max(xc - r, 0)), int(min(xc + r, SIZE))
ymin, ymax = int(max(yc - r, 0)), int(min(yc + r, SIZE))
for x in range(xmin, xmax):
for y in range(ymin, ymax):
z = (r ** 2) - ((x - xc) ** 2 + (y - yc) ** 2)
if z > 0:
terrain[x, y] += z
print("total iterations: {:d}".format(iter))
# normalize to unit height
zmin = np.min(terrain)
terrain -= zmin
zmax = np.max(terrain)
terrain /= zmax
# smooth the terrain by squaring the z values
terrain = np.power(terrain, 2)
# multiply by 255 so terrain can be visualized as grayscale image
terrain = terrain * 255
terrain = terrain.astype("uint8")
# convert mountains to valleys since stochastic gradient DESCENT
terrain = 255 - terrain
|
One possible terrain generated from the above code is shown below. I have also generated a contour map for the terrain.
1 2 3 4 5 6 7 8 9 | plt.title("terrain")
image = plt.imshow(terrain, cmap="gray")
plt.ylim(max(plt.ylim()), min(plt.ylim()))
plt.colorbar(image, shrink=0.8)
plt.title("contours")
contour = plt.contour(terrain, linewidths=2)
plt.ylim(max(plt.ylim()), min(plt.ylim()))
plt.colorbar(contour, shrink=0.8, extend='both')
|
 |
 |
Grid Search
As you can see, the terrain is just a matrix of shape (1024, 1024). Since our budget is 25 experiments, we will do a 5x5 grid search on this terrain. This means choosing 5 equidistant points on the x and y axes and reading the value of the terrain matrix at these (x, y) locations. The code to do this is shown below. We also show the points on the contour map. The best value among these points is circled in blue.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | # do a grid search (5x5)
results = []
for x in np.linspace(0, SIZE-1, 5):
for y in np.linspace(0, SIZE-1, 5):
xi, yi = int(x), int(y)
results.append([xi, yi, terrain[xi, yi]])
best_xyz = [r for r in sorted(results, key=operator.itemgetter(2))][0]
grid_best = best_xyz[2]
print(best_xyz)
xvals = [r[0] for r in results]
yvals = [r[1] for r in results]
plt.title("grid search")
contour = plt.contour(terrain, linewidths=2)
plt.ylim(max(plt.ylim()), min(plt.ylim()))
plt.scatter(xvals, yvals, color="b", marker="o")
plt.scatter([best_xyz[0]], [best_xyz[1]], color='b', s=200, facecolors='none', edgecolors='b')
plt.ylim(max(plt.ylim()), min(plt.ylim()))
plt.colorbar(contour)
|
The best result from the grid search is the point (767, 767) on the hyperparameter space and has a value of 109.
Random Search
Next up is pure random search. Since we have a budget of 25 experiments, we just generate random values of x and y and look up values of the terrain matrix at that point.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | # do a random search
results = []
xvals, yvals, zvals = [], [], []
for i in range(25):
x = np.random.randint(0, SIZE, 1)[0]
y = np.random.randint(0, SIZE, 1)[0]
results.append((x, y, terrain[x, y]))
best_xyz = sorted(results, key=operator.itemgetter(2))[0]
rand_best = best_xyz[2]
print(best_xyz)
xvals = [r[0] for r in results]
yvals = [r[1] for r in results]
plt.title("random search")
contour = plt.contour(terrain, linewidths=2)
plt.ylim(max(plt.ylim()), min(plt.ylim()))
plt.scatter(xvals, yvals, color="b", marker="o")
plt.scatter([best_xyz[0]], [best_xyz[1]], color='b', s=200, facecolors='none', edgecolors='b')
plt.colorbar(contour)
|
In this case the random search did a little better, finding the point (663, 618) whose value is 103.
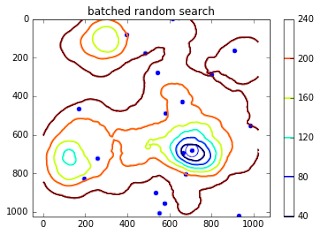
Batched Random Search
In this approach I decide to split my 25 experiment budget into 5 batches, each with 5 experiments. Looking up the (x, y) values are random within each batch. However, at the end of each batch, the winners (top 2 in my case) are singled out for special treatment. Instead of generating points anywhere in the space, we draw a window around these points and sample only from this space. At each iteration, the window shrinks geometrically. The intuition here is that I am trying to look for points in the neighborhood of the most optimal points found so far in the hope that this search will yield even more optimal points (exploitation). At the same time, I reserve the rest of the experiments to explore the space (exploration) in the hope that I might find another optimal point. The code for that is shown below:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | def cooling_schedule(n, k):
""" reduces jitter window size at each run
n - number of batches
k - index (0 based) of current batch
returns multiplier (0..1) of SIZE
"""
return (n - k) / n
results, winners = [], []
for bid in range(5):
print("Batch #: {:d}".format(bid), end="")
# compute window size
window_size = int(0.25 * cooling_schedule(5, bid) * SIZE)
# jitter the winners and add their values to results
# at any point we will only keep the top 2 global winners
for x, y, _, _ in winners:
if x < SIZE // 2:
# left of center
xleft = max(x - window_size // 2, 0)
xright = xleft + window_size
else:
# right of center
xright = min(x + window_size // 2, SIZE)
xleft = xright - window_size
if y < SIZE // 2:
# bottom half
ybot = max(y - window_size // 2, 0)
ytop = ybot + window_size
else:
# top half
ytop = min(y + window_size // 2, 0)
ybot = ytop - window_size
xnew = np.random.randint(xleft, xright, 1)[0]
ynew = np.random.randint(ybot, ytop, 1)[0]
znew = terrain[xnew, ynew]
results.append((xnew, ynew, znew, bid))
# add remaining random points
for i in range(5 - len(winners)):
x = np.random.randint(0, SIZE, 1)[0]
y = np.random.randint(0, SIZE, 1)[0]
z = terrain[x, y]
results.append((x, y, z, 2))
# find the top 2 global winners
winners = sorted(results, key=operator.itemgetter(2))[0:2]
print(" best: ", winners[0])
best_xyz = sorted(results, key=operator.itemgetter(2))[0]
print(best_xyz)
xvals = [r[0] for r in results]
yvals = [r[1] for r in results]
plt.title("batched random search")
contour = plt.contour(terrain, linewidths=2)
plt.ylim(max(plt.ylim()), min(plt.ylim()))
plt.scatter(xvals, yvals, color="b", marker="o")
plt.scatter([best_xyz[0]], [best_xyz[1]], color='b', s=200, facecolors='none', edgecolors='b')
plt.colorbar(contour)
|
This run ends up with the global minima in this space at (707, 682) with a value of 20.
Obviously, not all runs are this lucky, it is quite likely that the point found from any of the above approaches is just a local minima. Also there is no reason to assume that grid search might not outperform random search, since it is possible that a random terrain might have its global minima point right under one of the evenly laid out points, and a random search might miss that point.
In order to test that hypothesis, I ran the above code in batch for 1000 random terrains. For each terrain, I run 25 experiments for each of the 3 methods, and find the lowest (most optimal) point for each method. I count how many times one of the versions of random search outperform grid search over the 1000 random terrains. I did this twice just to make sure I didn't get the results by chance.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | TERRAIN_SIZE = 1024
NUM_HILLS = 200
NUM_TRIALS = 1000
NUM_SEARCHES_PER_DIM = 5
NUM_WINNERS = 2
nbr_random_wins = 0
nbr_brand_wins = 0
for i in range(NUM_TRIALS):
terrain = build_terrain(TERRAIN_SIZE, NUM_HILLS)
grid_result = best_grid_search(TERRAIN_SIZE, NUM_SEARCHES_PER_DIM)
random_result = best_random_search(TERRAIN_SIZE,
NUM_SEARCHES_PER_DIM**2)
batch_result = best_batch_random_search(TERRAIN_SIZE,
NUM_SEARCHES_PER_DIM,
NUM_SEARCHES_PER_DIM,
NUM_WINNERS)
print(grid_result, random_result, batch_result)
if random_result < grid_result:
nbr_random_wins += 1
if batch_result < grid_result:
nbr_brand_wins += 1
print("# times random search wins: {:d}".format(nbr_random_wins))
print("# times batch random search wins: {:d}".format(nbr_brand_wins))
|
Here are my results:
1 2 3 4 5 6 7 8 9 | Run-1
------
#-times random search wins: 619
#-times batch random search wins: 638
Run-2
------
#-times random search wins: 640
#-times batch random search wins: 621
|
So, it looks like random search seems to be slightly better than grid search (since the first number is more than 500). Also it looks like the batched version is not necessarily better since pure random search gave better results in the second run.
So anyway, thats what I had for today. This was mainly an exercise in convincing myself of something that didn't seem intuitively obvious to me. In the process, I learned an interesting algorithm to generate terrain, so that was quite a lot of fun as well. If you would like to run the code for yourself, the visualizations are in this IPython notebook, and the code for the batch run is in this python file.