A colleague recently started me off on this whole thing. We have been working on improving our indexing algorithms, and his (rhetorical) question was how anybody could assert (as we were hoping to assert) that the changes being made were improving (or going to improve) the quality of search. His point was that if you cannot measure it, you cannot manage it. As usual (at least for him), he had part of the solution worked out already - his ideas form the basis of the user-based scoring for precision calculations described below.
The E-Measure
Looking for some unrelated information on the web, I came across this paper by Jones, Robertson, Santimetvirul and Willet which contains a description of the E-Measure (or effectiveness measure) that can be used to quantify search quality, which looked about perfect for my purposes. The description of the E-Measure from the article is paraphrased below:
(1 + β2) * P * R
E(P,R) = 100 * (1 - ----------------)
(β2 * P) + R
where:
P = precision
R = recall
β = a coefficient indicating the relative importance of
precision vs recall. If set to 1.0, precision and
recall are equally important. If set to 2.0, precision
is twice as important as recall, etc.
For my own understanding, I drew some gnuplot charts of E against P and R, which I also include below - they may be helpful to you as well. As you can see, the quality of search is inversely related to the value of E, ie, if E goes down, search quality goes up, and vice versa. The best value for E appears to be when P and R are about equal (depending on the value of β, of course).

|
|

|
|
In this article, I describe how I calculate E for a given set of indexes built off the same corpus, each index corresponding to a block of iterative algorithmic changes in the index building code.
Calculating Recall
The formula for recall is r/T, where r is the number of relevant documents returned out of a total of T documents available for the given topic. It is not reasonable to compute T for every benchmark query, and in any case, my objective is to compare the increase or decrease in recall based on the original index. So, assuming a query Q on two different indexes, let r1 and r2 be the number of relevant documents returned:
R1 = r1 / T R2 = r2 / T Therefore: R2 / R1 = r2 / r1
Based on the above, I define R for an index as the normalized count of the average of the number of relevant results returned from all my benchmark queries against that given index.
Calculating Precision
The formula for precision is r/n, where r is the number of relevant documents returned from a total of n documents returned from a search. This is easy enough to calculate, but does not capture position information, ie, the fact that a good result at the top of the results is more valuable than one at the bottom.
For that, I use the index created before our code changes as the baseline index to measure precision. For each query in our set of benchmark queries, a human user scores the top 30 search results using a 5-point scale, -2 being the worst and +2 being the best. I consider only 30 because according to studies such as these, users rarely go beyond the 3rd page of search results. The scores are captured in a database table such as the one shown below:
1 2 3 4 5 6 7 8 9 | +-------------+--------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+-------------+--------------+------+-----+---------+-------+
| query_term | varchar(128) | NO | PRI | | |
| result_url | varchar(128) | NO | PRI | | |
| search_type | varchar(32) | NO | PRI | | |
| position | int(11) | NO | | | |
| score | int(11) | NO | | | |
+-------------+--------------+------+-----+---------+-------+
|
The overall precision for the index is calculated as the average of the sum of weighted scores for each query result, across all queries against that index. The weight reflects the importance of the score based on its position.
P = Σ (si * wi) / Nscored
where:
P = the precision of a given query
si = the score for result at position i
wi = atan(30 - i) / atan(30)
Nscored = number of results which were scored
The plot of the w(i) function for i=[0..29] is shown below. As you can see, the scores for the top results are going to be given a weight of 1, and the scores at the bottom will be deboosted

|
|
In addition, when issuing the same query against a new index created with an improved algorithm, we may find new results coming in to replace the existing results. These new results represent our uncertainity factor when calculating E. For search results for which we cannot find scores in the hon_scores table, we update an uncertainity metric using the max score possible, ie:
U = Σ (M * wi) / Nunscored
where:
U = the uncertainity for a given query
M = maximum score possible, in this case +2
wi = atan(30 - i) / atan(30)
i = position of the result about which we are uncertain
Nunscored = number of results which were unscored, ie new.
The value of U is used to calculate upper and lower bounds for the E-measure by calculating E(P+U, R) and E(P-U, R).
Calculating Effectiveness
Once the baseline scores are set up, a backend process runs all the benchmark queries through the other indexes in the collection (if not run already), and populates a table such as this one:
1 2 3 4 5 6 7 8 9 10 11 12 | +---------------+-------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+---------------+-------------+------+-----+---------+-------+
| index_name | varchar(32) | NO | PRI | | |
| search_type | varchar(32) | NO | PRI | | |
| prec | float(8,4) | NO | | | |
| uncertainity | float(8,4) | NO | | | |
| recall | float(8,4) | NO | | | |
| effectiveness | float(8,4) | NO | | | |
| effective_lb | float(8,4) | NO | | | |
| effective_ub | float(8,4) | NO | | | |
+---------------+-------------+------+-----+---------+-------+
|
Because the back-end code is part of a Spring web application, it is injected with quite a few specialized data access beans and if I had to show them all, this post would get very long. So I just provide pseudo-code for this job here. Essentially, all it is doing is executing a fixed set of queries against a fixed set of indexes, and looping through the results, looking for matches against the baseline, and calculating recall and precision appropriately..
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | for (indexName in indexNames):
searcher = buildSearcher(indexName)
precision, recall, uncertainity = 0
n_queryterms = 0
for (queryterm in queryterms):
hits = searcher.search(queryterm)
recall += hits.length
hits = hits[0,30]
position = n_scored = n_unscored = 0
query_precision = query_uncertainity = 0
for (hit in hits):
url = hit.url
weight = atan(30 - position) / atan(30)
if (url is scored):
query_precision += score * weight
n_scored++
else:
query_uncertainity += 2 * weight
n_unscored++
position++
# average for query
query_precision = query_precision / n_scored
query_uncertainity = query_uncertainity / n_unscored
n_queryterms++
precision += query_precision
uncertainity += query_uncertainity
# average precision and uncertainity for all query terms for a single index
precision = precision / n_queryterms
uncertainity = uncertainity / n_queryterms
# compute and save effectiveness (first pass)
save(recall, precision, uncertainity) for indexName
# After results for all indexes is populated, normalize recall so the max value
# across all indexes is 1
normalize_recall()
# Calculate e(p,r), e(p+u,r) and e(p-u,r) and save (second pass)
effectiveness = compute_e(p, r)
effectiveness_lowerbound = compute_e(p - u, r)
effectiveness_upperbound = compute_e(p + u, r)
# Save updated values (second pass)
save(recall, effectiveness,
effectiveness_lowerbound, effectiveness_upperbound)
for indexName
|
Graphing the Effectiveness measures
The chart(s) are generated dynamically off the data populated into the database by the backend process described above. I could have just used a table to display the results, but a graph makes things easier to visualize, and besides, I have been meaning to try out jfreechart for a while, and this seemed a good place to use it.
The code to allow the user to score individual search results and calculate the effectiveness scores are all part of a Spring web application, so I needed a way to show the graph on a web page. The controller just reads information off the table and builds a chart, converts it to a PNG bytestream and writes it into the response. The application allows scoring for different kinds of search, so multiple charts can be generated and shown on the same page.
Here is the code for the controller that generates the chart. The JFreeChart project has a pay-for-documentation business model, but there are any number of examples available on the web, which is where I got most of my information. I provide some comments in the code, but if you need more explanation, I would suggest looking at the many available JFreeChart examples.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 | // Source: src/main/java/com/mycompany/myapp/controllers/GraphController.java
package com.mycompany.myapp.controllers;
import java.awt.BasicStroke;
import java.awt.Color;
import java.awt.Paint;
import java.io.OutputStream;
import java.text.DecimalFormat;
import java.util.LinkedHashMap;
import java.util.List;
import java.util.Map;
import javax.servlet.http.HttpServletRequest;
import javax.servlet.http.HttpServletResponse;
import org.apache.commons.math.stat.descriptive.rank.Max;
import org.apache.commons.math.stat.descriptive.rank.Min;
import org.jfree.chart.ChartFactory;
import org.jfree.chart.ChartUtilities;
import org.jfree.chart.JFreeChart;
import org.jfree.chart.annotations.CategoryLineAnnotation;
import org.jfree.chart.axis.CategoryAxis;
import org.jfree.chart.axis.CategoryLabelPositions;
import org.jfree.chart.axis.NumberAxis;
import org.jfree.chart.labels.StandardCategoryItemLabelGenerator;
import org.jfree.chart.plot.CategoryPlot;
import org.jfree.chart.plot.PlotOrientation;
import org.jfree.chart.renderer.category.LineAndShapeRenderer;
import org.jfree.data.category.DefaultCategoryDataset;
import org.springframework.beans.factory.annotation.Required;
import org.springframework.web.bind.ServletRequestUtils;
import org.springframework.web.servlet.ModelAndView;
import org.springframework.web.servlet.mvc.Controller;
import com.mycompany.myapp.daos.EMeasureDao;
import com.healthline.util.Pair;
public class GraphController implements Controller {
private EMeasureDao emeasureDao;
@Required
public void setEmeasureDao(EMeasureDao emeasureDao) {
this.emeasureDao = emeasureDao;
}
public ModelAndView handleRequest(HttpServletRequest request,
HttpServletResponse response) throws Exception {
String searchType =
ServletRequestUtils.getRequiredStringParameter(request, "st");
List<Map<String,Object>> scoresForSearchType =
emeasureDao.getScoresForSearchType(searchType);
double minYe = Double.MAX_VALUE;
double maxYe = Double.MIN_VALUE;
double minYpr = Double.MAX_VALUE;
double maxYpr = Double.MIN_VALUE;
DefaultCategoryDataset prDataset = new DefaultCategoryDataset();
DefaultCategoryDataset eDataset = new DefaultCategoryDataset();
Map<String,Pair<Double,Double>> candlesticks =
new LinkedHashMap<String,Pair<Double,Double>>();
for (Map<String,Object> scoreForSearchType : scoresForSearchType) {
String indexName = (String) scoreForSearchType.get("INDEX_NAME");
Double precision = new Double((Float) scoreForSearchType.get("PREC"));
Double recall = new Double((Float) scoreForSearchType.get("RECALL"));
Double effectiveness =
new Double((Float) scoreForSearchType.get("EFFECTIVENESS"));
Double effectiveLb =
new Double((Float) scoreForSearchType.get("EFFECTIVE_LB"));
Double effectiveUb =
new Double((Float) scoreForSearchType.get("EFFECTIVE_UB"));
eDataset.addValue(effectiveness, "E-Measure", indexName);
prDataset.addValue(precision, "Precision", indexName);
prDataset.addValue(recall, "Recall", indexName);
candlesticks.put(indexName,
new Pair<Double,Double>(effectiveLb, effectiveUb));
minYe = min(new double[] {
minYe, effectiveness, effectiveLb, effectiveUb});
maxYe = max(new double[] {
maxYe, effectiveness, effectiveLb, effectiveUb});
minYpr = min(new double[] {minYpr, precision, recall});
maxYpr = max(new double[] {maxYpr, precision, recall});
}
JFreeChart chart = ChartFactory.createLineChart(
"", "Indexes", "E-Measure (%)", eDataset,
PlotOrientation.VERTICAL, true, true, false);
CategoryPlot plot = (CategoryPlot) chart.getPlot();
// show vertical gridlines
plot.setDomainGridlinePaint(Color.white);
plot.setDomainGridlineStroke(CategoryPlot.DEFAULT_GRIDLINE_STROKE);
plot.setDomainGridlinesVisible(true);
// customize domain (x-axis)
CategoryAxis domainAxis = plot.getDomainAxis();
domainAxis.setCategoryLabelPositions(CategoryLabelPositions.DOWN_45);
domainAxis.setTickLabelsVisible(true);
// customize range (y-axis).
NumberAxis rangeAxis = (NumberAxis) plot.getRangeAxis();
rangeAxis.setLowerBound(minYe == Double.MAX_VALUE ? 0.0D : minYe * 0.9D);
rangeAxis.setUpperBound(maxYe == Double.MIN_VALUE ? 200.0D :
maxYe * 1.1D);
rangeAxis.setLabelPaint(Color.red);
// display data values for e-measure
LineAndShapeRenderer renderer =
(LineAndShapeRenderer) plot.getRenderer();
DecimalFormat decimalFormat = new DecimalFormat("###.##");
renderer.setSeriesItemLabelGenerator(0,
new StandardCategoryItemLabelGenerator(
StandardCategoryItemLabelGenerator.DEFAULT_LABEL_FORMAT_STRING,
decimalFormat));
renderer.setSeriesPaint(0, Color.red);
renderer.setSeriesStroke(0, new BasicStroke(2.0F,
BasicStroke.CAP_ROUND, BasicStroke.JOIN_ROUND));
renderer.setSeriesItemLabelsVisible(0, true);
renderer.setBaseItemLabelsVisible(true);
plot.setRenderer(renderer);
// set candlestick annotations on e-measure for uncertainity
for (String indexName : candlesticks.keySet()) {
Pair<Double,Double> hilo = candlesticks.get(indexName);
plot.addAnnotation(new CategoryLineAnnotation(
indexName, hilo.getFirst(),
indexName, hilo.getSecond(),
Color.red,
new BasicStroke(2.0F, BasicStroke.CAP_ROUND,
BasicStroke.JOIN_ROUND)));
}
// add precision and recall with right hand side y-axis (0..2)
NumberAxis prRangeAxis = new NumberAxis("Precision/Recall");
prRangeAxis.setLowerBound(minYpr == Double.MAX_VALUE ? 0.0D :
minYpr * 0.9D);
prRangeAxis.setUpperBound(maxYpr == Double.MIN_VALUE ? 2.0D :
maxYpr * 1.1D);
plot.setRangeAxis(1, prRangeAxis);
plot.setDataset(1, prDataset);
plot.mapDatasetToRangeAxis(1, 1);
// display data values
Paint[] colors = new Paint[] {Color.green, Color.blue};
LineAndShapeRenderer prRenderer = new LineAndShapeRenderer();
DecimalFormat prDecimalFormat = new DecimalFormat("#.##");
for (int i = 0; i < 2; i++) {
prRenderer.setSeriesItemLabelGenerator(i,
new StandardCategoryItemLabelGenerator(
StandardCategoryItemLabelGenerator.DEFAULT_LABEL_FORMAT_STRING,
prDecimalFormat));
prRenderer.setSeriesPaint(i, colors[i]);
prRenderer.setSeriesStroke(i, new BasicStroke(2.0F,
BasicStroke.CAP_ROUND, BasicStroke.JOIN_ROUND));
prRenderer.setSeriesItemLabelsVisible(i, true);
}
prRenderer.setBaseItemLabelsVisible(true);
plot.setRenderer(1, prRenderer);
// output to response
OutputStream responseOutputStream = response.getOutputStream();
ChartUtilities.writeChartAsPNG(responseOutputStream, chart, 750, 400);
responseOutputStream.flush();
responseOutputStream.close();
return null;
}
private double max(double[] values) {
Max max = new Max();
return max.evaluate(values);
}
private double min(double[] values) {
Min min = new Min();
return min.evaluate(values);
}
}
|
The Controller is called from an image tag from the JSP page like this. That way we can have multiple image tags and they are all started off in parallel while the page is loaded.
1 | <img src="/honscorer/_graph.do"/>
|
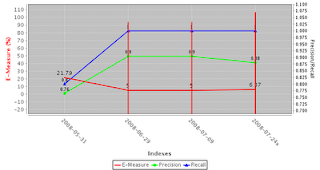
As we can see from the chart above, both recall and precision increased initially from the baseline index, and the E-Measure came down from 21.79 to 5, but then some algorithm change between 2008-07-09 and 2008-07-24x caused a slight decrease in the precision and a slight uptick in the E-Measure. I think automated search quality metrics such as these can be quite useful as an early warning system for unexpected side effects caused by some algorithm change, as well as a way to measure how a change or set of changes affect the overall search quality.















Be the first to comment. Comments are moderated to prevent spam.
Post a Comment